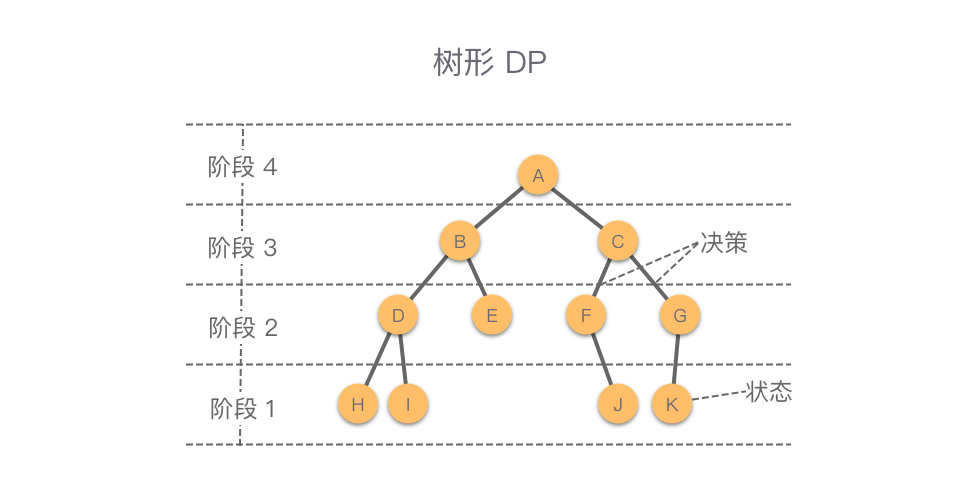
树形动态规划:简称为「树形 DP」,是一种在树形结构上进行推导的动态规划方法。如下图所示,树形 DP 的求解过程一般以节点从深到浅(子树从小到大)的顺序作为动态规划的「阶段」。在树形 DP 中,第
$1$ 维通常是节点编号,代表以该节点为根的子树。
树形 DP 问题的划分方法有多种方式。
如果按照「阶段转移的方向」进行划分,可以划分为以下两种:
- 自底向上:通过递归的方式求解每棵子树,然后在回溯时,自底向上地从子节点向上进行状态转移。只有在当前节点的所有子树求解完毕之后,才可以求解当前节点,以及继续向上进行求解。
- 自顶向下:从根节点开始向下递归,逐层计算子节点的状态。这种方法常常使用记忆化搜索来避免重复计算,提高效率。
自顶向下的树形 DP 问题比较少见,大部分树形 DP 都是采用「自底向上」的方向进行推导。
如果按照「是否有固定根」进行划分,可以划分为以下两种:
-
固定根的树形 DP:事先指定根节点的树形 DP 问题,通常只需要从给定的根节点开始,使用
$1$ 次深度优先搜索。 -
不定根的树形 DP:事先没有指定根节点的树形 DP 问题,并且根节点的变化会对一些值,例如子节点深度和、点权和等产生影响。通常需要使用
$2$ 次深度优先搜索,第$1$ 次预处理诸如深度,点权和之类的信息,第$2$ 次开始运行换根动态规划。
本文中,我们将按照「是否有固定根」进行分类,对树形 DP 问题中这两种类型问题进行一一讲解。
下面以这两道题为例,介绍一下树形 DP 的一般解题思路。
描述:给定一个长度为
要求:找出路径上任意一对相邻节点都没有分配到相同字符的最长路径,并返回该路径的长度。
说明:
-
$n == parent.length == s.length$ 。 -
$1 \le n \le 10^5$ 。 - 对所有
$i \ge 1$ ,$0 \le parent[i] \le n - 1$ 均成立。 -
$parent[0] == -1$ 。 -
$parent$ 表示一棵有效的树。 -
$s$ 仅由小写英文字母组成。
示例:
- 示例 1:
输入:parent = [-1,0,0,1,1,2], s = "abacbe"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:0 -> 1 -> 3 。该路径的长度是 3 ,所以返回 3。
可以证明不存在满足上述条件且比 3 更长的路径。- 示例 2:
输入:parent = [-1,0,0,0], s = "aabc"
输出:3
解释:任意一对相邻节点字符都不同的最长路径是:2 -> 0 -> 3 。该路径的长度为 3 ,所以返回 3。因为题目给定的是表示父子节点的
如果不考虑相邻节点是否为相同字符这一条件,那么这道题就是在求树的直径(树的最长路径长度)中的节点个数。
对于根节点为
- 如果其最长路径经过根节点
$u$ ,则$最长路径长度 = 某子树中的最长路径长度 + 另一子树中的最长路径长度 + 1$ 。 - 如果其最长路径不经过根节点
$u$ ,则$最长路径长度 = 某个子树中的最长路径长度$ 。
即:$最长路径长度 = max(某子树中的最长路径长度 + 另一子树中的最长路径长度 + 1, \quad 某个子树中的最长路径长度)$。
对此,我们可以使用深度优先搜索递归遍历
- 先计算出从相邻节点
$v$ 出发的最长路径长度$v\underline{}len$ 。 - 更新维护全局最长路径长度为
$self.ans = max(self.ans, \quad u\underline{}len + v\underline{}len + 1)$ 。 - 更新维护当前节点
$u$ 的最长路径长度为$u\underline{}len = max(u\underline{}len, \quad v\underline{}len + 1)$ 。
因为题目限定了「相邻节点字符不同」,所以在更新全局最长路径长度和当前节点
最后,因为题目要求的是树的直径(树的最长路径长度)中的节点个数,而:$路径的节点 = 路径长度 + 1$,所以最后我们返回
class Solution:
def longestPath(self, parent: List[int], s: str) -> int:
size = len(parent)
# 根据 parent 数组,建立有向图
graph = [[] for _ in range(size)]
for i in range(1, size):
graph[parent[i]].append(i)
ans = 0
def dfs(u):
nonlocal ans
u_len = 0 # u 节点的最大路径长度
for v in graph[u]: # 遍历 u 节点的相邻节点
v_len = dfs(v) # 相邻节点的最大路径长度
if s[u] != s[v]: # 相邻节点字符不同
ans = max(ans, u_len + v_len + 1) # 维护最大路径长度
u_len = max(u_len, v_len + 1) # 更新 u 节点的最大路径长度
return u_len # 返回 u 节点的最大路径长度
dfs(0)
return ans + 1-
时间复杂度:$O(n)$,其中
$n$ 是树的节点数目。 - 空间复杂度:$O(n)$。
描述:给定一个整数
要求:返回一个大小为
说明:
- 两个城市间距离:定义为它们之间需要经过的边的数目。
- 一棵子树:城市的一个子集,且子集中任意城市之间可以通过子集中的其他城市和边到达。两个子树被认为不一样的条件是至少有一个城市在其中一棵子树中存在,但在另一棵子树中不存在。
-
$2 \le n \le 15$ 。 -
$edges.length == n - 1$ 。 -
$edges[i].length == 2$ 。 -
$1 \le u_i, v_i \le n$ 。 - 题目保证
$(ui, vi)$ 所表示的边互不相同。
示例:
- 示例 1:
输入:n = 4, edges = [[1,2],[2,3],[2,4]]
输出:[3,4,0]
解释:
子树 {1,2}, {2,3} 和 {2,4} 最大距离都是 1 。
子树 {1,2,3}, {1,2,4}, {2,3,4} 和 {1,2,3,4} 最大距离都为 2 。
不存在城市间最大距离为 3 的子树。- 示例 2:
输入:n = 2, edges = [[1,2]]
输出:[1]因为题目中给定
而对于一个确定的子树来说,求子树中两个城市间距离就是在求子树的直径,这就跟 「1245. 树的直径」 和 「2246. 相邻字符不同的最长路径」 一样了。
那么这道题的思路就变成了:
- 通过二进制枚举的方式,得到所有子树。
- 对于当前子树,通过树形 DP + 深度优先搜索的方式,计算出当前子树的直径。
- 统计所有子树直径中经过的不同边数个数,将其放入答案数组中。
class Solution:
def countSubgraphsForEachDiameter(self, n: int, edges: List[List[int]]) -> List[int]:
graph = [[] for _ in range(n)] # 建图
for u, v in edges:
graph[u - 1].append(v - 1)
graph[v - 1].append(u - 1)
def dfs(mask, u):
nonlocal visited, diameter
visited |= 1 << u # 标记 u 访问过
u_len = 0 # u 节点的最大路径长度
for v in graph[u]: # 遍历 u 节点的相邻节点
if (visited >> v) & 1 == 0 and mask >> v & 1: # v 没有访问过,且在子集中
v_len = dfs(mask, v) # 相邻节点的最大路径长度
diameter = max(diameter, u_len + v_len + 1) # 维护最大路径长度
u_len = max(u_len, v_len + 1) # 更新 u 节点的最大路径长度
return u_len
ans = [0 for _ in range(n - 1)]
for mask in range(3, 1 << n): # 二进制枚举子集
if mask & (mask - 1) == 0: # 子集至少需要两个点
continue
visited = 0
diameter = 0
u = mask.bit_length() - 1
dfs(mask, u) # 在子集 mask 中递归求树的直径
if visited == mask:
ans[diameter - 1] += 1
return ans-
时间复杂度:$O(n \times 2^n)$,其中
$n$ 为给定的城市数目。 - 空间复杂度:$O(n)$。